
| Schnitt | erwartete Eingaben | berechnete Ergebnisse |
|---|---|---|
| Geraden- schnitt |
je zwei beliebige Punkte auf jeder der beiden zu schneidenden Geraden | Gemeinlot definiert durch zwei Punkte, je einer auf jeder Geraden, die minimalen Abstand haben, außerdem die Abstände dieser Punkte von den gegebenen Punkten. Ein negativer Abstand bedeutet, dass der Gemeinlotendpunkt nicht zwischen den gegebenen Punkten liegt. Schließlich erhält man noch den Mittelpunkt des Gemeinlots und dessen Länge. |
| Vorwärts- schnitt |
je ein beliebiger Punkt auf sowie Richtungs- und Zenitwinkel von jeder der beiden zu schneidenden Strahlen | wie Geradenschnitt, jedoch nur ein Abstand pro Gerade. Ein negativer Abstand bedeutet, dass der Gemeinlotendpunkt nicht auf dem Strahl, sondern entgegengesetzt zur Blickrichtung liegt. |
| Rückwärts- schnitt |
je ein beliebiger Punkt auf sowie Horizontal- und Zenitwinkel von jeder der drei zu schneidenden Strahlen. | alle möglichen Schnittpunkte, jedoch keine Schnittpunkte entgegengesetzt zur Blickrichtung, außerdem die Koordinaten aller Punkte im Standpunktsystem jedes Schnittpunktes. |
| Kugel- schnitt |
drei Mittelpunkte von Kugeln und drei Radien (Distanzen zum Schnittpunkt) | alle möglichen Schnittpunkte |
| oder |
vier Mittelpunkte von Kugeln und vier Pseudodistanzen, die von den Radien (Distanzen zum Schnittpunkt) um denselben unbekannten Offset abweichen | alle möglichen Schnittpunkte, wobei solche, für die sich negative Distanzen ergeben würden, durchgestrichen sind, außerdem die zugehörigen Offsets |
| Gerade/ Ebene |
zwei beliebige Punkte auf der Geraden, danach drei beliebige Punkte auf der Ebene | Schnittpunkt sowie Abstände von den gegebenen Punkten auf der Geraden. Ein negativer Abstand bedeutet,dass der Schnittpunkt nicht zwischen den gegebenen Geradenpunkten liegt. |
| oder | nur ein beliebiger Punkt auf dem Strahl, aber zusätzlich Richtungs- und Zenitwinkel des Strahls | Schnittpunkt sowie Abstand vom gegebenen Punkt auf dem Strahl. Ein negativer Abstand bedeutet, dass der Schnittpunkt nicht auf dem Strahl, sondern entgegengesetzt zur Blickrichtung liegt. |
| oder | zwei beliebige Punkte auf der Geraden, danach ein beliebiger Punkte auf der Ebene, aber zusätzlich Richtungs- und Zenitwinkel des Normalenvektors der Ebene | Schnittpunkt sowie Abstände von den gegebenen Punkten auf der Geraden. Ein negativer Abstand bedeutet, dass der Schnittpunkt nicht zwischen den gegebenen Geradenpunkten liegt. |
| oder | nur je ein beliebiger Punkt auf dem Strahl und auf der Ebene, zusätzlich Richtungs- und Zenitwinkel des Strahls und des Normalenvektors der Ebene | Schnittpunkt sowie Abstand vom gegebenen Punkt auf dem Strahl. Ein negativer Abstand bedeutet, dass der Schnittpunkt nicht auf dem Strahl, sondern entgegengesetzt zur Blickrichtung liegt. |
| oder | wie zuvor, aber statt Winkeln die Vektorkomponenten des Geradenvektors und danach des Normalenvektors der Ebene | wie zuvor |
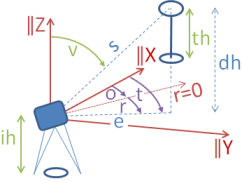
Bei den geodätischen Schnitten, die durch gemessene Richtungen oder Winkel definiert werden, beziehen sich diese Messwerte auf die Achsen des Systems der gegebenen Koordinaten.
Ausnahme:
Beim Rückwärtssschnitt beziehen sich die gemessenen Winkel auf die Achsen eines Standpunktsystems x,y,z,
die nicht zu den Achsen des Systems der gegebenen Koordinaten X,Y,Z parallel sein müssen.
Jeder mögliche Schnittpunkte hat in der Regel ein anderes Standpunktsystem.
In jedem dieser Standpunktsysteme werden für alle gegebenen Punkte Koordinaten berechnet.
| Schnitt | Existenz und Eindeutigkeit |
|---|---|
| Geraden- und Vorwärts- schnitt |
Da zwei Geraden im Raum in der Regel windschief sind, existiert meist kein Schnittpunkt. Jedoch existiert das Gemeinlot, außer bei parallelen Geraden, und ist eindeutig. Sollte tatsächlich ein Schnittpunkt existieren, hat das Gemeinlot die Länge Null. Es kann aber sein, dass die Lage des Schnittpunktes oder Gemeinlots als unzulässig angesehen wird. Beim Vorwärtsschnitt werden diese Lage meist in Blickrichtung vorausgesetzt. Sind die Geraden parallel, wird nichts berechnet. |
| Rückwärts- schnitt |
Möglicherweise existiert kein Schnittpunkt. Andernfalls sind ein bis vier Schnittpunkte möglich. |
| Kugel- schnitt |
Möglicherweise existiert kein Schnittpunkt, aber wenn doch, dann in der Regel zwei Schnittpunkte. Bei Pseudodistanzen kann es sein, dass nach Abzug des berechneten Offsets eine oder mehrere Distanz negativ sind. Sollte das als unzulässig anzusehen sein, wäre dieser Schnittpunkt zu verwerfen. |
| Gerade/ Ebene |
Wenn Gerade und Ebene parallel sind, wird nichts berechnet. Andernfalls gibt es einen eindeutigen Schnittpunkt. Es kann aber sein, dass die Lage des Schnittpunktes oder Gemeinlots als unzulässig angesehen wird. Bei gegebenen Winkeln oder gegebenem Geradenvektor wird diese Lage meist in Blickrichtung vorausgesetzt. |
Berechnete Schnittpunkte oder Endpunkte von Gemeinloten können in andere Rechenwerkzeuge geladen werden, z.B. in .
Beim Rückwärtssschnitt ist zwischen dem System der gegebenen Punkte und dem Standpunktsystem, in welchem die Messwerte aufgenommen wurden, zu unterscheiden. Um die Transformationsparameter zwischen beiden Systemen zu ermitteln, werden die Koordinaten aller Punkte auch im Standpunktsystem berechnet, so dass diese in geladen werden können. Falls es mehrere mögliche Schnittpunkte gibt, ist das Standpunktsystem in der Regel für jeden Schnittpunkt ein anderes.
| Punkt- | X | Y | Z |
|---|---|---|---|
| name | |||
| A | 9 | 27 | 15 |
| B | 0 | 3 | 0 |
| C | 12 | 0 | 27 |
Ein regelmäßiges Tetraeder ist ein Polyeder, welches von vier gleichseitigen Dreiecksflächen begrenzt wird. Die rechts aufgelisteten drei Punkte A,B,C bilden ein gleichseitiges Dreieck mit der Seitenlänge √882,
| Punkt- | X | Y | Z |
|---|---|---|---|
| name | |||
| D1 | -15 | 12 | 24 |
| D2 | 29 | 8 | 4 |
Kugelschnitt: A,B,C sollen durch einen vierten Eckpunkt D zu einem regelmäßiges Tetraeder ABCD ergänzt werden. Der Punkt D kann über den Schnitt dreier Kugeln um die Mittelpunkte A,B,C mit den Radien von jeweils √882 erzeugt werden. Wir erhalten die zwei Lösungen D1 und D2 rechts.
| Ziel- | Hz- | Zenit- |
|---|---|---|
| name | Richtung | winkel |
| A | 0° | 0° |
| B | 60° | 0° |
| C | 30° | arctan(√0.5) |
Rückwärtsschnitt: Wenn man im Punkt D Richtungsmessungen so macht, dass der Horizontalkreis des Messgeräts in der Ebene ABD mit Nullpunkt nach A ausrichtet ist, würde man die rechts aufgelisteten Horizontalrichtungen und Zenitwinkel messen. Somit kann der Punkt D auch über einen Rückwärtsschnitt berechnet werden. Dabei ergibt sich aber nur der Schnittpunkt D2(29;8;4). Um den Schnittpunkt D1(-15;12;24) zu erhalten, müsste man entweder A und B vertauschen oder bei C den Zenitwinkel 180°-arctan(√0.5) angeben.
Aus den Standpunktkoordinaten liest man auch die Höhe des Tetraeders ab: A,B,D spannen die xy-Ebene auf, haben also z=0 und C hat z=24.2487.
Wir verwenden im Weiteren D2 als D.
| Punkt | Hz- | Zenit- | |
|---|---|---|---|
| name | Richtung | winkel | |
| @A°B | 4.5 | 15.0 | 7.5 |
| Mittel | 12.5 | 9.5 | 11.5 |
| @C°D | 20.5 | 4.0 | 15.5 |
Geradenschnitt: Gegenüberliegende Kanten sind windschief, schneiden sich also nicht. Man kann aber mittels Geradenschnitt deren Gemeinlot berechnen, das ist hier die Verbindungsstrecke zwischen den Kantenmittelpunkten. Der Mittelpunkt des Gemeinlots ist gleichzeitig der Mittelpunkt des Tetraeders M(12.5;9.5;11.5).
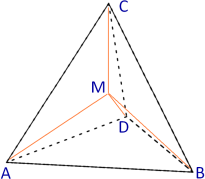
Das Gemeinlot hat die Länge 21. Die vier Abstände der Gemeinlotendpunkte sind alle gleich 14.8592=√220.5, was beweist, dass die Kantenmittelpunkte verbunden werden. Durch Änderung der Reihenfolge der Punkte A,B,C,D in der Koordinatenliste in A,C,B,D erhält man das andere Gemeinlot.
Kugelschnitt mit Pseudodistanzen: Den Mittelpunkt M des Tetraeders können wir auch so konstruieren, dass wir einen Kugelschnitt von gleich großen Kugeln um die Eckpunkte berechnen. Wenn wir alle vier Eckpunkte wählen, müssen wir auch gar nicht den Radius kennen. Wir arbeiten einfach mit vier gleichen Pseudodistanzen, z.B. 0;0;0. Die Radien erhält man dann über den Offset, der in dem Fall negativ wäre. (Der Offset ist der Wert, der zu den Radien bei der gedachten Pseudodistanzmessung addiert wird.)
Wir erhalten zwei identische Schnittpunkte, die dem schon per Geradenschnitt erhaltenen Mittelpunkt M des Tetraeders entsprechen. Einer von ihnen gehört allerdings zu vier Kugeln mit ''negativen'' Radien und wird deshalb ignoriert. Der Offset2 von -18.1865 bedeutet, dass die Abstände des Mittelpunktes M von den Eckpunkten alle 18.1865 betragen.
Schnitt Gerade/Ebene: Den Mittelpunkt einer Tetraederseitenfläche können wir auch so konstruieren, dass wir das Lot vom gegenüberliegenden Punkt mit dieser Ebene schneiden. Die Seitenfläche ABC definieren wir über die Punkte A,B,C. Das zugehörige Lot definieren wir über die Punkte D,M.
Für den Mittelpunkt der Seite ABC werden die Koordinaten 7;10;14 erhalten. Der Schnittwinkel ist erwartungsgemäß -90°. Der Winkel ist negativ, weil im Linkssystem die Punkte A,B,C gegen den Uhrzeigersinn angeordnet sind. Blickrichtung ist dabei von D über M. (Im Rechtssystem wäre es umgekehrt.)
Der Abstand Schnittpunkt ⇒ M ist negativ, woraus man erkannt, dass der Schnittpunkt von D aus gesehen hinter M liegt. Der Abstand D ⇒ Schnittpunkt entspricht der zuvor schon ermittelten Höhe des Tetraeders.
berechnet auch eine Ebene durch drei Punkte oder eine Kugel durch vier Punkte. Gewichte sind dann egal, können auch fehlen. Wenn Sie die Abstände weiterer Punkte von der Fläche und/oder ihre Projektionen auf die Fläche benötigen, geben Sie diese als zu projizierende Punkte an. Die Abstände berechnen Sie als Längen der Differenzvektoren.
Eine andere Lösung für die Kugel durch vier Punkte ist mittels und dem Kugelschnitt mit vier Pseudodistanzen möglich. Man gibt die vier Punkte als Mittelpunkte von vier Kugeln mit identischen Pseudodistanzen an, am einfachsten mit 0;0;0;0. Der Radius der gesuchten Kugel ist die sich ergebende viermal identische Distanz. Der Mittelpunkt der gesuchten Kugel ist der sich ergebende Schnittpunkt der vier Kugeln. Der praktische Vorteil dieser Methode ist, dass dieser Mittelpunkt direkt in eine Koordinatenliste geladen werden kann. (Rechnerisch ergeben sich allerdings zwei identische Schnittpunkte, einer mit ''negativem'' Radius gleichen Betrags, der verworfen werden kann.)
|
|
|
|